Distance Vector Algorithm
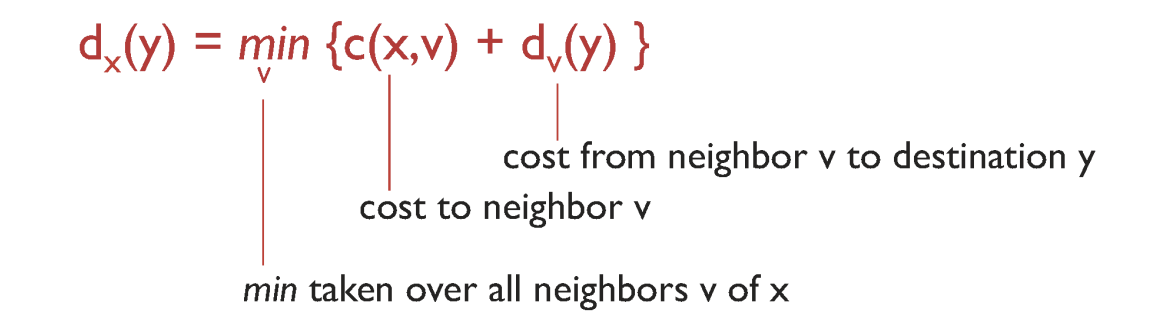
- x- y 최소 비용 경로( dx(y) ) ⇒ 이웃한 모든 정점 v에서 y로 가는 최소 비용 + x에서 v로 가는 최소 비용의 최솟값
- 인접한 라우터 정보만 알고있다.
- 각 라우터는 자신이 알고 있는 distance vector(array)를 이웃한 라우터에게 넘겨준다.
- 자신의 distance vector을 넘겨주는 조건은 distance vactor들 중 값이 하나라도 업데이트 된다면 전달한다. 또는 직접적으로 연결된 링크의 cost가 변경된 경우 distance를 계산해서 값이 바뀌었으면 전달한다.
- 전달하고 전달받아 계산하는, 이러한 과정들이 반복되다보면 어느순간 stable(안정적인 상황, 거리가 다 계산된 상황)하게 된다.
Distance Vector 예시
- 각 라우터는 이웃한 라우터와 DV를 교환한다.

- 이웃한 라우터의 DV를 받고 Bellman-Ford equation을 사용하여 추정된 비용이 감소했으면 distance vector를 수정한다.

- DV의 변화가 없을 때까지 반복한다.

Distance Vector의 문제점
count-to-infinity
- 라우팅 프로토콜에서 라우터들이 끊어진 연결이나 장애를 판단하고 이를 공유하는데 걸리는 무한한 시간이 걸리는 문제
“무한한 시간”은 실제 시간이 무한대로 걸리는 것이 아니라, 네트워크 상태가 안정화되기까지 너무 많은 시간이 소요되는 상황을 나타낸다. 이 문제는 특히 변경 사항(링크 실패 등)이 라우팅 시스템 전체로 빠르게 전파되지 않아, 라우터들이 노드 사이의 최단 경로를 정확하게 계산하는데 오랜 시간이 걸리게 되는 경우에 발생한다.

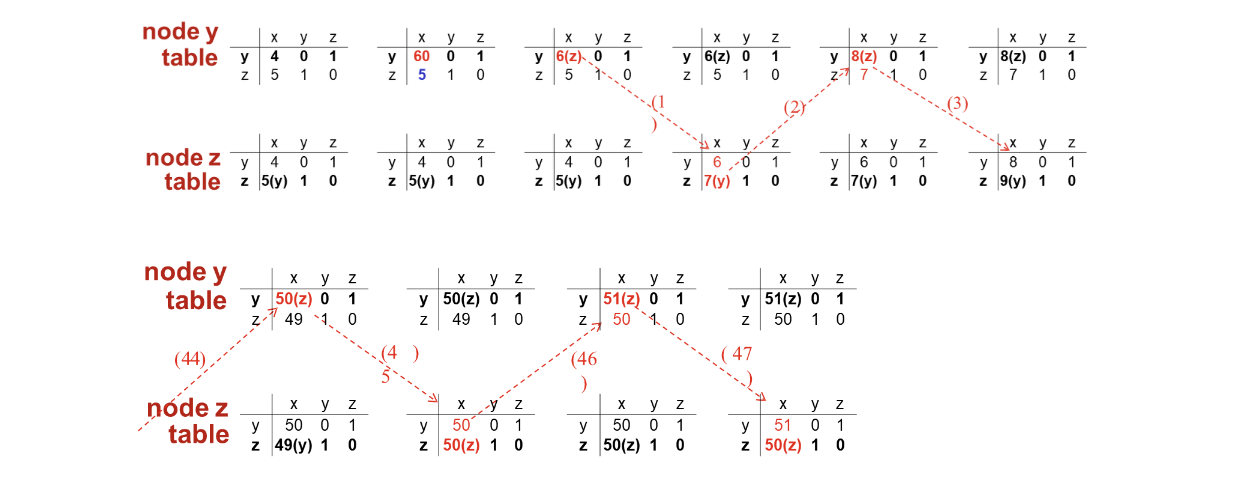
- x - y의 거리가 2에서 60으로 업데이트 되었다고 가정해보자.
- y테이블: x로 가는 최단 경로 → y - z - x
- z테이블: x로 가는 최단 경로 → z - y - x
- y는 본인이 가진 테이블을 참조하여 x로 최단경로로 보내기 위해 z로 보내고 z는 x로 최단으로 보내기 위해 y로 보낸다. y는 z가 최단 경로를 가지고 있으므로 z에게 보낸다. 이 과정이 y에서 x로 가는 최소 비용 경로가 51이 될 때까지 반복되게 된다.
- 수가 더 커진다면 더 많은 참조가 발생하게 되고 안정화 상태까지 시간이 오래걸리게 된다.
- z에서 x로 가는 최소 경로 dz(x)가 y를 거쳐 가는 길이기 때문에 이와 같은 상황이 발생한다.
- z는 y → x 경로 비용이 수정되었다는걸 모르기 때문이다.
해결방법
1️⃣ Split horizon
- 정보가 들어온 곳으로 같은 정보를 보낼 수 없다 .
- z가 x로 도착하기 위해서 y를 거쳐야하는 경우, z는 y에게 z - y - x 의 거리를 알려주지 않는 것
2️⃣ Poisoned reverse
- 정보가 들어온 곳으로 정보를 보낼 수 있으나 경로의 비용을 무한대로 설정하여 보낸다.
- z가 x로 도착하기 위해서 y를 거쳐야하는 경우, z는 y에게 z - y- x의 거리가 무한대라고 알려주는 것
3️⃣ Hold Down
- 라우터가 라우트(경로)의 상태 변화(특히 라우트의 실패)를 감지했을 때, 일정 시간 동안 그 라우트에 대한 모든 업데이트를 무시하도록 한다.
- 네트워크가 안정 상태로 돌아올 시간을 제공하고, 라우팅 테이블에서 무한 숫자 문제가 발생하는 것을 방지할 수 있다.
벨만-포드 vs 다익스트라
- 다익스트라
- 매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하여 한 단계씩 최단 거리를 구해나간다.
- 음수 간선이 없다면 최적의 해를 찾을 수 있다. (음수 간선이 있을 때는 최적의 해를 찾을 수 없다)
- 시간 복잡도가 빠르다.
- 벨만-포드 알고리즘
- (정점 - 1)번의 매 단계마다 모든 간선을 전부 확인하면서 모든 노드 간의 최단 거리를 구해나간다.
- 다익스트라와 차이점은 매 반복마다 모든 간선을 확인한다는 것이다. 다익스트라는 방문하지 않는 노드 중에서 최단 거리가 가장 가까운 노드만을 방문한다.
- 다익스트라 알고리즘에서의 최적의 해를 항상 포함하게 된다.
- 음수 간선이 있어도 최적의 해를 찾을 수 있다. (음수 간선의 순환을 감지할 수 있기 때문이다)
- 시간 복잡도가 느리다.
- (정점 - 1)번의 매 단계마다 모든 간선을 전부 확인하면서 모든 노드 간의 최단 거리를 구해나간다.
[Network] Routing algorithms - Distance Vector
컴퓨터 네트워크_30_ Distance vector routing algorithm
'📝Computer Science > network' 카테고리의 다른 글
| 링크 계층(1) _ MAC, CSMA, CSMA/CD (0) | 2023.07.20 |
|---|---|
| 네트워크 계층(6) _ AS (Autonomous System), BGP (0) | 2023.07.18 |
| 네트워크 계층(4) _ ICMP, Routing Algorithm, Link-State Routing Algorithm (0) | 2023.07.17 |
| 네트워크 계층(3) _ DHCP, MTU, IP 단편화 (0) | 2023.07.17 |
| 네트워크 계층(2) _ IP, IP Address, CIDR, Subnet, NAT (1) | 2023.07.13 |



