[python] 힙(heap)과 힙큐(heapq)란?

 힙(heap) 

• 최댓값과 최솟값을 빠르게 찾기 위해 고안된 자료구조
• 완전 이진트리
• 힙 property
  • A가 B의 부모노드이면 A의 키값과 B의 키값 사이에는 대소 관계가 성립한다.

최소 힙

• 부모 노드의 키값이 자식 노드의 키값보다 항상 작은 힙

최대 힙

• 부모 노드의 키값이 자식 노드의 키값보다 항상 큰 힙

 

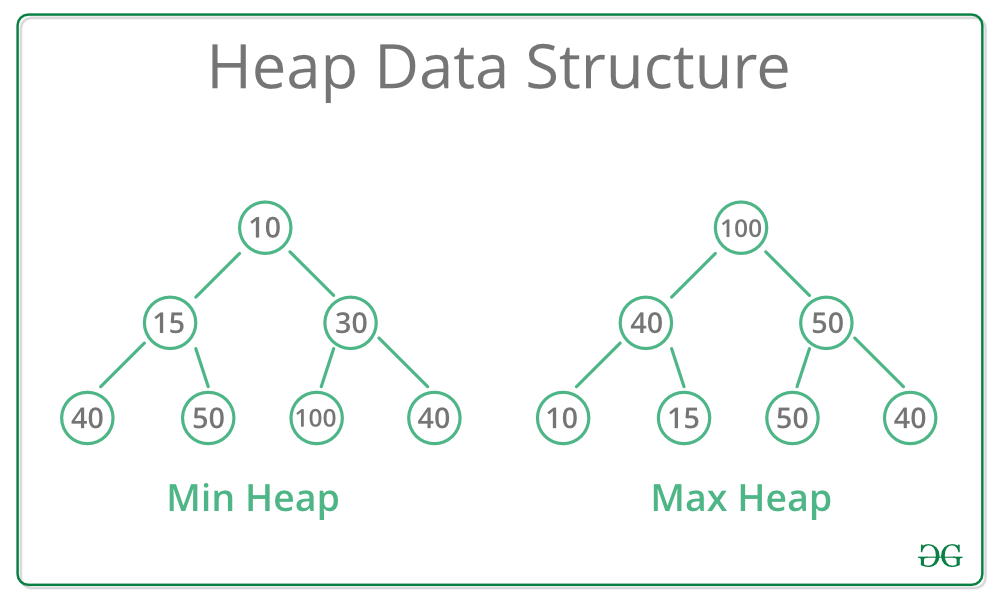
• 힙에서는 가장 낮은(혹은 높은) 우선순위를 가지는 노드가 항상 루트에 오게 된다.
  • 이를 이용해 우선순위 큐와 같은 추상적 자료형을 구현할 수 있다.
• 키 값의 대소 관계
  • 부모/자식 노드 ⭕
  • 형제노드 ❌
• 시간복잡도
  • O(log n)

---

 최소힙(heapq 모듈을 사용하지 않고 구현) 

# 최소힙

# 힙 삽입 연산
def heap_push(item):
    heap.append(item)
    child = len(heap) - 1
    parent = child // 2

    # 루트 노드이거나 최소힙 조건을 만족하지 못하면 종료
    while parent > 0 and heap[parent] > heap[child]:
        heap[parent], heap[child] = heap[child], heap[parent]
        child = parent
        parent = child // 2

# 힙 삭제 연산
def heap_pop():
    # 루트 노드만 남은 경우 바로 반환
    if len(heap) <= 2:
        return heap.pop()

    item = heap[1]  # 루트 노드 백업
    heap[1] = heap.pop()  # 마지막 노드를 루트 노드로 이동
    parent = 1
    child = parent * 2

    while child < len(heap):  # 자식이 하나라도 있으면
        if child + 1 < len(heap) and heap[child] > heap[child + 1]:
            # 오른쪽 자식이 있고, 오른쪽 자식이 왼쪽 자식보다 작다면
            child += 1  # 비교 대상을 오른쪽 자식으로 갱신

        # 자식이 더 작으면 최소힙이 아니므로 노드 교환
        if heap[parent] > heap[child]:
            heap[parent], heap[child] = heap[child], heap[parent]
            parent = child
            child = parent * 2
        # 최소힙 만족하면 탈출
        else:
            break

    return item  # 백업했던 루트 노드 반환

heap = [0]
heap_push(2)
heap_push(5)
heap_push(7)
heap_push(3)
heap_push(4)
heap_push(6)
print(heap)

while len(heap) >= 2:
    print(heap_pop())

---

 최대힙(heapq 모듈을 사용하지 않고 구현) 

# 최대힙

# 힙 삽입 연산
def heap_push(item):
    heap.append(item)
    child = len(heap) - 1
    parent = child // 2

    # 루트 노드이거나 최대힙 조건을 만족하지 못하면 종료
    while parent > 0 and heap[parent] < heap[child]:
        heap[parent], heap[child] = heap[child], heap[parent]
        child = parent
        parent = child // 2

# 힙 삭제 연산
def heap_pop():
    # 루트 노드만 남은 경우 바로 반환
    if len(heap) <= 2:
        return heap.pop()

    item = heap[1]  # 루트 노드 백업
    heap[1] = heap.pop()  # 마지막 노드를 루트 노드로 이동
    parent = 1
    child = parent * 2

    while child < len(heap):  # 자식이 하나라도 있으면
        if child + 1 < len(heap) and heap[child] < heap[child + 1]:
            # 오른쪽 자식이 있고, 오른쪽 자식이 왼쪽 자식보다 크다면
            child += 1  # 비교 대상을 오른쪽 자식으로 갱신

        # 자식이 더 크면 최대힙이 아니므로 노드 교환
        if heap[parent] < heap[child]:
            heap[parent], heap[child] = heap[child], heap[parent]
            parent = child
            child = parent * 2
        # 최대힙 만족하면 탈출
        else:
            break

    return item  # 백업했던 루트 노드 반환

heap = [0]
heap_push(2)
heap_push(5)
heap_push(7)
heap_push(3)
heap_push(4)
heap_push(6)
print(heap)

while len(heap) >= 2:
    print(heap_pop())

 

---

 힙큐(heapq) 

• 파이썬 heapq 모듈은 heapq 알고리즘을 제공한다.
• 이진 트리 기반의 최소 힙(min heap) 자료구조를 제공한다.
  • min heap을 사용하면 원소들이 항상 정렬된 상태로 추가되고 삭제된다.
  • min heap에서 가장 작은 값은 언제나 인덱스 0 즉, 이진 트리의 루트에 위치한다.
  • 내부적으로 min heap 내의 모든 원소(k)는 항상 자식 원소들 (2k+1, 2k+2)보다 크기가 작거나 같도록 원소가 추가되고 삭제된다.

heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2]

     1  ---> root
   /   \\
  3     5
 / \\   /
4   8 7

---

 heapq 모듈을 이용한 최소힙 

from heapq import heappush, heappop

heap = []

heappush(heap, 2)
heappush(heap, 5)
heappush(heap, 7)
heappush(heap, 3)
heappush(heap, 4)
heappush(heap, 6)
print(heap)

while heap:
    print(heappop(heap))

• heapq 모듈은 파이썬의 보통 리스트를 마치 최소 힙처럼 다룰 수 있도록 도와준다.
  • 파이썬에서는 heapq 모듈을 통해서 원소를 추가하거나 삭제한 리스트가 그냥 최소 힙이라는 것!

---

 heapq 모듈을 이용한 최대 힙 

from heapq import heappush, heappop

nums = [4, 1, 7, 3, 8, 5]
heap = []

for num in nums:
  heappush(heap, (-num, num))  # (우선 순위, 값)

while heap:
  print(heappop(heap)[1])  # index 1

8
7
5
4
3
1

---

 힙에 원소 추가 

heappush()

from heapq import heappush

heappush(heap, 4)
heappush(heap, 1)
heappush(heap, 7)
heappush(heap, 3)
print(heap)

[1, 3, 7, 4]

• 가장 작은 1 이 인덱스 0에 위치한다.
• 인덱스 1(=k)에 위치한 3 은 인덱스 3(=2k+1)에 위치한 4 보다 크므로 힙의 공식을 만족한다.

---

 힙에서 원소 삭제 

heappop()

from heapq import heappop

print(heappop(heap))
print(heap)

1
[3, 4, 7]

• 가장 작았던 1 이 삭제되어 리턴되었고, 그 다음으로 작았던 3 이 인덱스 0이 되었다.

---

 최소값 삭제하지 않고 얻기 

• 리스트의 첫번째 원소에 접근하듯이 인덱스를 통해서 접근하면 된다!

# [3, 4, 7]
print(heap[0]) # 3

⚠️ 주의사항

• 힙(Heap)은 완전 이진 트리의 일종으로, 특별한 순서를 유지하는 배열이다.
• 힙은 부모 노드가 자식 노드보다 작은 값을 갖도록 구성된 완전 이진 트리이다. 그러나 트리의 레벨별로 순서가 보장되어 있는 것은 아니다!
• 인덱스 0에 가장 작은 원소가 있다고 해서 인덱스 1에 두 번째로 작은 원소, 인덱스 2에 세 번째로 작은 원소가 있다는 보장은 없다!
• 힙은 heappop() 함수를 호출하여 원소를 삭제할 때마다 이진 트리의 재배치를 통해 매번 새로운 최솟값을 인덱스 0에 위치시킨다.
• 따라서 두 번쨰로 작은 원소를 얻으려면 heap[1] 으로 접근하면 안되고, 반드시 heappop() 을 통해 가장 작은 원소를 삭제 후에 heap[0] 을 통해 새로운 최솟값에 접근해야한다.

---

 기존 리스트를 힙으로 변환 

heapify()

from heapq import heapify

heap = [4, 1, 7, 3, 8, 5]
heapify(heap)
print(heap)

[1, 3, 5, 4, 8, 7]

 

• heapify() 는 새로운 리스트를 반환하는 것이 아니라 인자로 넘긴 리스트에 직접 변경한다.
  • 따라서 원본 리스트의 형태를 보존해야하는 경우에는 반드시 해당 리스트를 복제한 후에 인자로 넘겨야 한다!

nums = [4, 1, 7, 3, 8, 5]

heap = nums[:]
heapify(heap)

print(nums)
print(heap)

[4, 1, 7, 3, 8, 5]
[1, 3, 5, 4, 8, 7]

 

---

 응용 

 n번째 최솟값/최댓값 

nsmallest()

• 주어진 리스트에서 가장 작은 n 개의 값을 담은 리스트를 반환한다.
  • 반환된 리스트의 마지막 값이 n 번째 작은 값이 된다.

from heapq import nsmallest

nsmallest(3, [4, 1, 7, 3, 8, 5])[-1]

 

nlargest()

• n 번재 최댓값을 구한다.

from heapq import nlargest

nlargest(3, [4, 1, 7, 3, 8, 5])[-1]

---

 힙 정렬 

from heapq import heappush, heappop

def heap_sort(nums):
  heap = []
  for num in nums:
    heappush(heap, num)

  sorted_nums = []
  while heap:
    sorted_nums.append(heappop(heap))
  return sorted_nums

print(heap_sort([4, 1, 7, 3, 8, 5]))

[1, 3, 4, 5, 7, 8]

 

 

---

참고자료

https://www.daleseo.com/python-heapq/

파이썬의 heapq 모듈로 힙 자료구조 사용하기